Map
classDiagram Map <.. HashTable: 实现 Dictionary <-- HashTable: 继承 HashTable <-- Properties: 继承 Map <.. EnumMap: 实现 AbstractMap <-- EnumMap: 继承 AbstractMap <-- HashMap: 继承 AbstractMap <-- TreeMap: 继承 HashMap <-- LinkedHashMap: 继承 Map <.. HashMap: 实现 Map <.. AbstractMap: 实现 Map <.. SortedMap: 实现 SortedMap <.. NavigableMap: 实现 NavigableMap <.. TreeMap: 实现HashMap
- 允许 null 值,不同于 HashTable ,是线程不安全的
- load factor(影响因子) 默认值是 0.75, 是均衡了时间和空间损耗算出来的值
- 如果有很多数据需要储存到 HashMap 中,建议 HashMap 的容量一开始就设置成足够的大小,这样可以防止在其过程中不断的扩容,影响性能
- 在迭代过程中,如果 HashMap 的结构被修改,会快速失败
架构
操作
- 新增
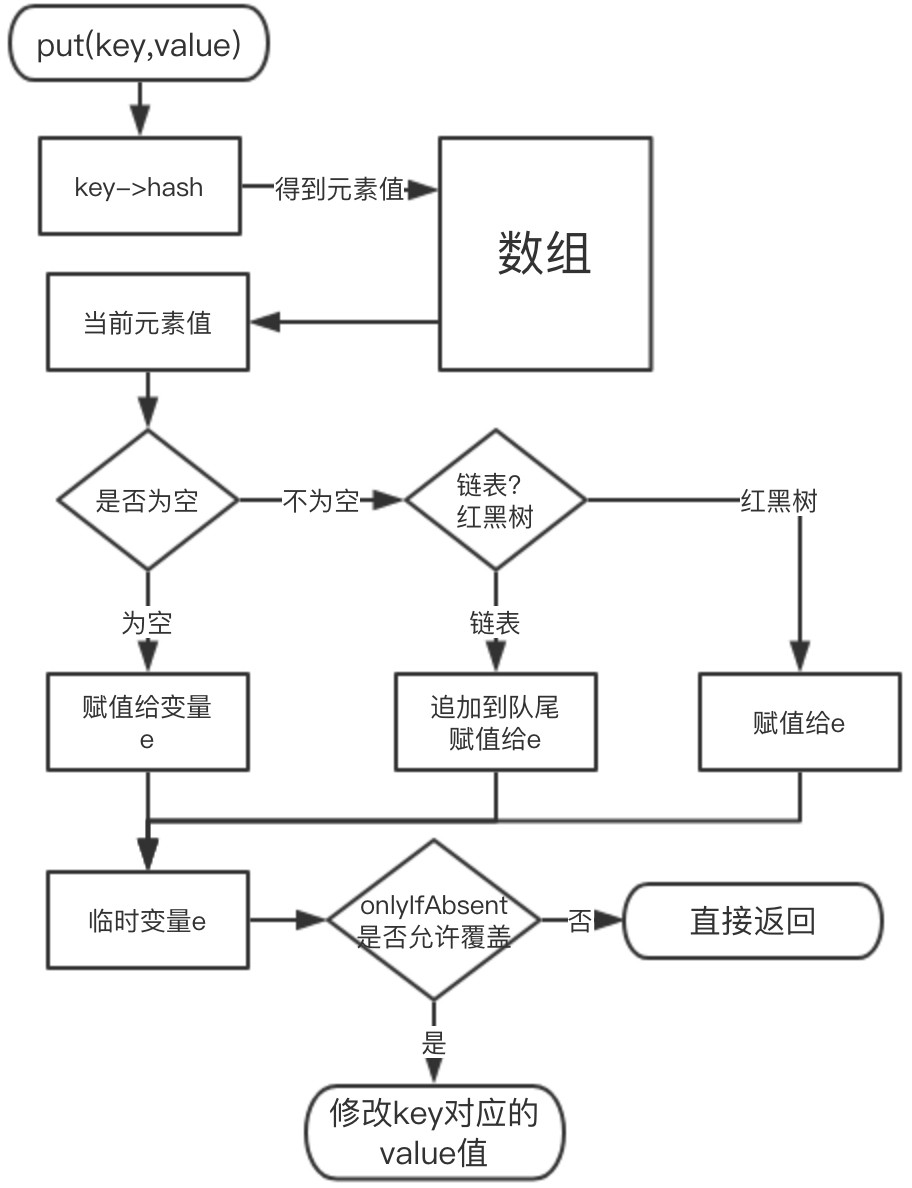
1.空数组有无初始化,没有的话初始化;2.如果通过 key 的 hash 能够直接找到值,跳转到 6,否则到 3;3.如果 hash 冲突,两种解决方案:链表 or 红黑树;4.如果是链表,递归循环,把新元素追加到队尾;5.如果是红黑树,调用红黑树新增的方法;6.通过 2、4、5 将新元素追加成功,再根据 onlyIfAbsent 判断是否需要覆盖;7.判断是否需要扩容,需要扩容进行扩容,结束。
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { Node<K,V>[] tab; Node<K,V> p; int n, i; // 如果数组为空,那就初始化数组 if ((tab = table) == null || (n = tab.length) == 0) n = (tab = resize()).length; // 如果根据hashCode得到的索引位置为空,直接将新节点放到该节点 if ((p = tab[i = (n - 1) & hash]) == null) tab[i] = newNode(hash, key, value, null); else { Node<K,V> e; K k; // 如果现在索引位置的hash值与key都相等,直接将新节点放在这里 if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) e = p; // 否则就需要追加节点到当前索引位置节点的后面(链表或者红黑树) // 如果是红黑树,那就调用红黑树的增加方法 else if (p instanceof TreeNode) e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); else { // 否则就是链表,进行遍历 for (int binCount = 0; ; ++binCount) { if ((e = p.next) == null) { p.next = newNode(hash, key, value, null); if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st treeifyBin(tab, hash); break; } // 当遍历的节点hash值与key都相等时,那新节点就是放在这里 if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break; p = e; } } // 这里的e如果不为null,那就代表插入的这个key中是有值得,根据传入的onlyIfAbsent决定是否覆盖 if (e != null) { // existing mapping for key V oldValue = e.value; if (!onlyIfAbsent || oldValue == null) e.value = value; afterNodeAccess(e); return oldValue; } } // 维护HashMap的其他状态信息 ++modCount; if (++size > threshold) // size达到一定的程度,就需要扩容 resize(); afterNodeInsertion(evict); return null;}链表转为红黑树
只有当链表长度大于等于8,并且整个数组长度大于等于64时,才会进行链表转红黑树
至于为什么是8,链表查询的时间复杂度是 O (n),红黑树的查询复杂度是 O (log (n))。在链表数据不多的时候,使用链表进行遍历也比较快,只有当链表数据比较多的时候,才会转化成红黑树,但红黑树需要的占用空间是链表的 2 倍,考虑到转化时间和空间损耗,8是最合适的
在元素放置过程中,恶意构造哈希冲突的数据是有可能的,针对于JDK8之前使用链表来存储相同哈希的数据可以进行哈希碰撞拒绝服务攻击,消耗服务端的CPU
红黑树的插入
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab, int h, K k, V v) { Class<?> kc = null; boolean searched = false; // 找到根节点 TreeNode<K,V> root = (parent != null) ? root() : this; // 遍历 for (TreeNode<K,V> p = root;;) { int dir, ph; K pk; // 说明应该插在当前遍历节点的右子树 if ((ph = p.hash) > h) dir = -1; // 说明应该插在当前遍历节点的左子树 else if (ph < h) dir = 1; // 找到跟插入节点相等的节点,返回 else if ((pk = p.key) == k || (k != null && k.equals(pk))) return p; // 实现了Comparable,通过compareTo比较 else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) { if (!searched) { TreeNode<K,V> q, ch; searched = true; if (((ch = p.left) != null && (q = ch.find(h, k, kc)) != null) || ((ch = p.right) != null && (q = ch.find(h, k, kc)) != null)) return q; } dir = tieBreakOrder(k, pk); } // 插入新节点 TreeNode<K,V> xp = p; if ((p = (dir <= 0) ? p.left : p.right) == null) { Node<K,V> xpn = xp.next; TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn); if (dir <= 0) xp.left = x; else xp.right = x; xp.next = x; x.parent = x.prev = xp; if (xpn != null) ((TreeNode<K,V>)xpn).prev = x; moveRootToFront(tab, balanceInsertion(root, x)); return null; } }}着色是指红黑树的节点着上红色或黑色,旋转是为了让红黑树更加平衡,提高查询的效率,总的来说都是为了满足红黑树的 5 个原则:
- 节点是红色或黑色
- 根是黑色
- 所有叶子都是黑色
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点
- 从每个叶子到根的所有路径上不能有两个连续的红色节点
- 查找
1.根据 hash 算法定位数组的索引位置,equals 判断当前节点是否是我们需要寻找的 key,是的话直接返回,不是的话往下。2.判断当前节点有无 next 节点,有的话判断是链表类型,还是红黑树类型。3.分别走链表和红黑树不同类型的查找方法链表查找
do { // 遍历,看遍历的节点的key是否与查找的key相等 if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) return e;} while ((e = e.next) != null);红黑树查找
final TreeNode<K,V> find(int h, Object k, Class<?> kc) { TreeNode<K,V> p = this; do { int ph, dir; K pk; TreeNode<K,V> pl = p.left, pr = p.right, q; // hash比当前节点小,往左子树寻找 if ((ph = p.hash) > h) p = pl; // hash比当前节点大,往左右树寻找 else if (ph < h) p = pr; // 找到了 else if ((pk = p.key) == k || (k != null && k.equals(pk))) return p; // 左子树为空,所以只能向右子树找 else if (pl == null) p = pr; // 右子树为空,所以只能左右子树找 else if (pr == null) p = pl; // 使用compareTo比较 else if ((kc != null || (kc = comparableClassFor(k)) != null) && (dir = compareComparables(kc, k, pk)) != 0) p = (dir < 0) ? pl : pr; else if ((q = pr.find(h, k, kc)) != null) return q; else p = pl; } while (p != null); return null;}TreeMap
TreeMap 底层的数据结构就是红黑树,TreeMap 利用了红黑树左节点小,右节点大的性质,根据 key 进行排序,使每个元素能够插入到红黑树大小适当的位置,维护了 key 的大小关系
- 新增
public V put(K key, V value) { Entry<K,V> t = root; // 根节点为空,直接将插入节点作为根节点 if (t == null) { compare(key, key); // type (and possibly null) check root = new Entry<>(key, value, null); size = 1; modCount++; return null; } int cmp; Entry<K,V> parent; // split comparator and comparable paths Comparator<? super K> cpr = comparator; if (cpr != null) { // 遍历找到插入节点应该插入的位置,parent保存了该位置的父节点 do { parent = t; cmp = cpr.compare(key, t.key); if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); } else { // 实现了Comparable的情况下的比较 if (key == null) throw new NullPointerException(); @SuppressWarnings("unchecked") Comparable<? super K> k = (Comparable<? super K>) key; do { parent = t; cmp = k.compareTo(t.key); if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); } Entry<K,V> e = new Entry<>(key, value, parent); if (cmp < 0) parent.left = e; else parent.right = e; fixAfterInsertion(e); size++; modCount++; return null;}LinkedHashMap
LinkedHashMap 本身是继承 HashMap 的,所以它拥有 HashMap 的所有特性,再此基础上,还提供了两大特性:
- 按照插入顺序进行访问;
- 实现了访问最少最先删除功能
按照插入顺序新增
// 通过在创建新节点时,把这个节点加到一个链表的最尾部来维护插入顺序Node<K,V> newNode(int hash, K key, V value, Node<K,V> e) { LinkedHashMap.Entry<K,V> p = new LinkedHashMap.Entry<>(hash, key, value, e); linkNodeLast(p); return p;}private void linkNodeLast(LinkedHashMap.Entry<K,V> p) { LinkedHashMap.Entry<K,V> last = tail; tail = p; if (last == null) head = p; else { p.before = last; last.after = p; }}按照插入顺序访问
// 跟链表的迭代器一样final LinkedHashMap.Entry<K,V> nextNode() { LinkedHashMap.Entry<K,V> e = next; if (modCount != expectedModCount) throw new ConcurrentModificationException(); if (e == null) throw new NoSuchElementException(); current = e; next = e.after; return e;}最少访问删除的实现
在get之后,LinkedHashMap会对获取到的节点执行移到链表尾部的操作
public V get(Object key) { Node<K,V> e; if ((e = getNode(hash(key), key)) == null) return null; if (accessOrder) afterNodeAccess(e); return e.value;}// 这段代码是负责把e移到末尾// 这样就队头的元素就是访问最少的元素void afterNodeAccess(Node<K,V> e) { // move node to last LinkedHashMap.Entry<K,V> last; if (accessOrder && (last = tail) != e) { LinkedHashMap.Entry<K,V> p = (LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after; p.after = null; if (b == null) head = a; else b.after = a; if (a != null) a.before = b; else last = b; if (last == null) head = p; else { p.before = last; last.after = p; } tail = p; ++modCount; }}问题
HashMap 底层数据结构
底层采用了数组、链表、红黑树来实现的
数组的主要作用是查找,时间复杂度为O(1),默认大小16,元素存放的下标是根据key的hashCode计算出来的
元素存放在Node里面,当key的hashCode一样时,但是key并不相等,Node就会串起来,形成链表,链表的时间复杂度是O(N)
当链表长度大于等于8且数组长度大于等于64时,链表就会转成红黑树,红黑树的时间复杂度为O(lg n)
HashMap、TreeMap、LinkedHashMap 三者有啥相同点,有啥不同点
相同点:
- 都使用了红黑树
- hash算法相同
- 都非线程安全
不同点:
- HashMap数据结构以数组为主,查询速度快,TreeMap利用了红黑树左小右大的特点,可以实现对key的排序,LinkedHashMap则增加了链表的结构,实现了顺序访问以及最少访问删除
hash算法
n=array.length;tab[i = (n - 1) & hash]取模算法的好处,就是可以保证计算出来的索引下标值可以均匀的分布在数组的各个索引位置上
当 b 是 2 的幂次方时,a % b = a &(b-1)
解决hash冲突的办法
- 好的hash算法
- 自动扩容
- 冲突后使用链表与红黑树
HashMap 是如何扩容的
- put时,发现数组为空,初始化扩容,默认大小16
- put成功后,发现数组大于现在数组的容量*0.75,会进行扩容,每次扩容为原来数组大小的两倍
- 扩容之后,需要对数组中的Node节点重新计算hash值,重新放置
对象作为 Map 的 key 时,需要注意的点
一定需要覆写 equals 和 hashCode 方法,如果是 TreeMap 的话,需要实现 Comparable 接口